El ying y el yang de los modelos analíticos

EQUILIBRIO SESGO-VARIANZA

Como ya dijimos en otros artículos del blog , uno de los pilares fundamentales en aprendizaje automático o Machine Learning es la comprensión del equilibrio sesgo-varianza, y ver cómo podemos gestionarlo en nuestro modelo predictivo. Para entenderlo, tenemos que saber que los datos, por lo general, serán divididos en dos grandes grupos: un conjunto de entrenamiento, usado para entrenar a nuestro modelo para mejorar su rendimiento, y un conjunto de test, destinado a probar cómo de bueno es el modelo a la hora de enfrentarse ante datos que no vio cuando fue entrenado (será nuestro proxy a datos del futuro que están por analizar).

¡¡No caigáis en la tentación de usar todos los datos para entrenar al modelo, pensando en el “cuantos más mejor”, ni extrapoléis el error en el entrenamiento al error que se tendrá en la realidad, pues es bastante probable que ese no sea el caso!!

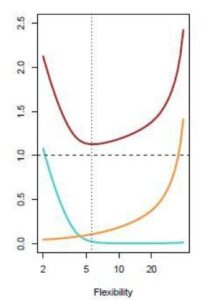
Dicho esto vamos a centrarnos en el error del conjunto de test, ya que no olvidemos el objetivo último del modelo: la aplicación en casos futuros. Para entenderlo mejor vamos a utilizar la siguiente gráfica, extraída del recomendable libro An Introduction to Statistical Learning.

Si nos fijamos en el error total (línea roja), mientras dotamos al modelo de más flexibilidad, va disminuyendo (el modelo es capaz de captar mejor la función que trata de replicar). Sin embargo, llega un momento en el que la flexibilidad es contraproducente en este conjunto de test, pues empieza a aumentar de nuevo, ¿qué quiere decir esto? Que el modelo tiene tanta flexibilidad que se adaptó muy bien a los datos de entrenamiento. Tan bien, que lo que obtuvimos fue una solución ad hoc para ese conjunto, generalizando muy mal ante casos futuros (como vemos en el error de test)

Podemos intuir que la línea roja es la suma del resto de líneas:

• La línea azul indica el error de sesgo, debido a que el modelo carece de la flexibilidad óptima para capturar la función de los datos (pensemos en tratar de explicar una nube de datos en forma circular mediante un modelo lineal).
• La línea amarilla indica el error de varianza, achacable a cuánto varía el modelo en caso de cambiar el conjunto de entrenamiento (si el modelo se adapta perfectamente al conjunto de entrenamiento, al cambiar el conjunto, cambiará hasta ajustarse al nuevo conjunto, siendo buena solución para el conjunto de entrenamiento, pero mala generalización para datos futuros).
• La línea continua permanece inalterable a medida que aumenta la flexibilidad. Se refiere al error irreducible, y nos recuerda el desgraciado hecho de que cualquier modelo va a tener un error al aplicarlo en datos futuros, es decir, en la realidad.

Como vemos, ser capaces de encontrar el punto donde el error total se minimice será la tarea primordial del analista, que tendrá que buscar en el equilibrio sesgo-varianza aquella solución que mejor le permita extrapolar su análisis al escenario real.