¿Cómo predecir consumos con algoritmos de Machine Learning?

Siguiendo el post de la semana pasada que servía de introducción a los algoritmos de Machine Learning , se realizará una predicción de consumos. Partiendo de consumos pasados, se tratará de predecir los futuros y ver cómo se ajusta la predicción a la realidad.

Para ello se analizarán los datos de los que se dispone, qué es la estacionalidad y en qué afecta a los algoritmos de aprendizaje y por último la elección del algoritmo y su programación en lenguaje R.

Machine Learning – Predicción de consumos

El objetivo final de esta serie de post será conseguir adelantarse a eventos futuros y, de esta forma, poder anticipar los recursos necesarios en la empresa para hacer frente tanto a los picos como a los valles en las ventas.

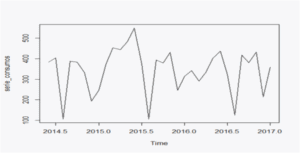
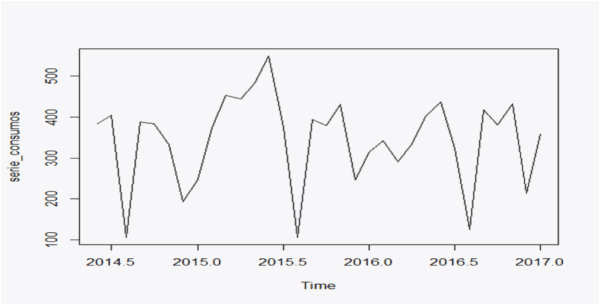
A continuación, se muestra la gráfica de los consumos:

¿Qué datos necesitamos para poder predecir utilizando algoritmos de Machine Learning?

Se dispone de los datos de ventas agrupados por mensualidades, datando los más antiguos, de Junio del 2014, y los más recientes, de Enero del 2017, por lo que se busca realizar una predicción de 9 meses. Se dispone además de los datos reales entre los meses de Febrero y Octubre del 2017 para, una vez realizada la predicción, poder comparar con los resultados de la misma.

Series estacionarias y series que tienen estacionalidad

El estudio de la serie temporal de la que se dispone es una de las complejidades del proceso de selección del algoritmo de predicción.

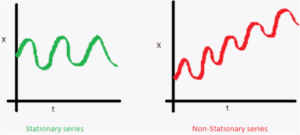
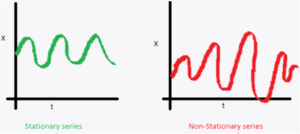
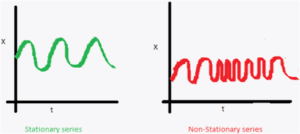
Lo primero de todo, es determinar si la serie es o no estacionaria (stationary serie o non-stationary serie). La gran mayoría de los algoritmos de predicción están diseñados para realizar las predicciones sobre series estacionarias; por lo que es muy importante entender cómo es una serie estacionaria. Como se puede ver en este enlace, se puede identificar de manera gráfica si nuestra serie es o no estacionaria. Existen tres criterios para poder clasificar si la serie es o no estacionaria:

• La media de la serie temporal no debe tener dependencia del tiempo, es decir, debe de ser constante. Como se muestra en la imagen adjunta, la gráfica verde se corresponde con la gráfica estacionaria, donde podemos ver que la media es constante, mientras que en la gráfica roja se puede observar que la media va aumentando en función del tiempo.

• La varianza de la serie temporal debe de ser constante, es decir, no debe variar en función del tiempo. Como en el caso anterior, la gráfica verde correspondería a una serie estacionaria, frente a la no estacionaria en rojo. En la primera de ellas, la varianza es constante, mientras que en la segunda la varianza varía con el tiempo, ya que, como se observa, la diferencia entre los máximos y los mínimos es mayor en la zona central de la gráfica roja.

• El último criterio, está relacionado con la covarianza entre un punto “i” de la serie temporal y el punto “(i+m)”. En estos puntos, la covarianza debe ser constante en el tiempo. Como se puede observar, la gráfica roja no cumple este requisito dado que se “encoge” y “alarga” en función del tiempo, mientras que la gráfica verde tiene todos los máximos y los mínimos a la misma distancia.

Otro de los puntos importantes a la hora de aplicar un algoritmo de predicción es saber si la serie tiene estacionalidad (seasonal serie o non-seasonal serie). Es decir, es importante desestacionalizar la serie para eliminar los periodos de más o menos ventas, como puede ser la temporada de verano o la de invierno.

Tras estudiar los consumos representados en la primera de las gráficas, es fácil observar que esta serie no es estacionaria y tampoco tiene una estacionalidad marcada, simplemente se vende menos en Agosto y en Diciembre.

El algoritmo que se utilizará debido a las propiedades identificadas en el proceso anterior, se localiza en el programa estadístico R y se trata de la función “auto.arima”. Esta función de R trabaja con series estacionarias o no y con series que tengan o no una estacionalidad marcada.

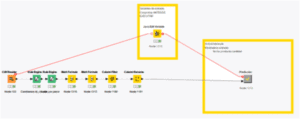
Por último, se utilizará Knime con la integración de R. Aquí se encuentra otro post relacionado con Knime y R. A continuación se muestra una imagen de cómo quedaría la interfaz gráfica en Knime:

Arima como algoritmo de predicción

Por consiguiente, para realizar una predicción de ventas, donde sólo se dispone de las ventas a pasado, un algoritmo fácil de utilizar es el algoritmo Arima. Por ello, como ya hemos comentado, para utilizar este algoritmo se recurre a la función de R “auto.arima”. Esta función trabaja tanto con series estacionarias o no estacionarias y con series que tengan una estacionalidad marcada o no. Por todo ello, esta función de R es la elegida para realizar esta predicción.

En el próximo post…

En el post de la semana que viene, se representarán los resultados de manera gráfica y se comparará la predicción realizada con los consumos reales durante los meses evaluados.

COMPARTE ESTE POST

Share on facebook
Share on google
Share on twitter
Share on linkedin
Share on pinterest
Share on print
Share on email