Algoritmo PCA: de lo complejo a lo sencillo

Cuando alguien se encuentra ante una situación compleja, siempre se trata de simplificar el problema.

El algoritmo CPA trata de simplificar el problema inicial, para poder ir resolviéndolo de la forma más sencilla a la más compleja. A la vez que se va adquiriendo la experiencia necesaria para solventar el problema inicial.

CPA, Reducción de variables

Partiendo de un problema con múltiples variables, se busca entender qué relación existe entre ellas. Para ello, el primer paso será reducir al máximo posible las variables de las que se dispone. Una vez conseguido este paso, representaremos de manera visual el resultado obtenido y así podremos observar cómo se agrupan los datos de manera fácil e intuitiva.

Se dispone de un archivo csv que almacena el histórico de unas órdenes de compra de unas piezas. El objetivo de este análisis de datos es agrupar las piezas que, por características, estén unas próximas a las otras, es decir, que se encuentren cercanas unas de otras en el espacio. Hacer esto en un espacio de 12 Dimensiones no es sencillo ni representable gráficamente. Para ello, se plantean reducir el número de variables al menor número posible de ellas. Para llevar a cabo este cambio, se decide utilizar una técnica matemática conocida como “Análisis de Componentes Principales”.

¿Qué es un “Análisis de Componentes Principales” o PCA? y ¿para qué sirve?

Es un método matemático que se utiliza para reducir el número de variables de forma que pasemos a tener el mínimo número de nuevas variables y que representen a todas las antiguas variables de la forma más representativa posible. Es decir, si se reduce el número de variables a dos o tres nuevas, se pueden representar los datos originales en el plano o en un gráfico de 3-dimensiones y, así, se visualiza de forma gráfica un resumen de nuestros datos. El simple hecho de poder tener los datos de manera visible simplifica mucho el entender qué puede estar pasando y ayuda a tomar decisiones.

A continuación, se procede con el análisis de las órdenes de compra. No se entrará en los detalles puramente matemáticos dada su complejidad.

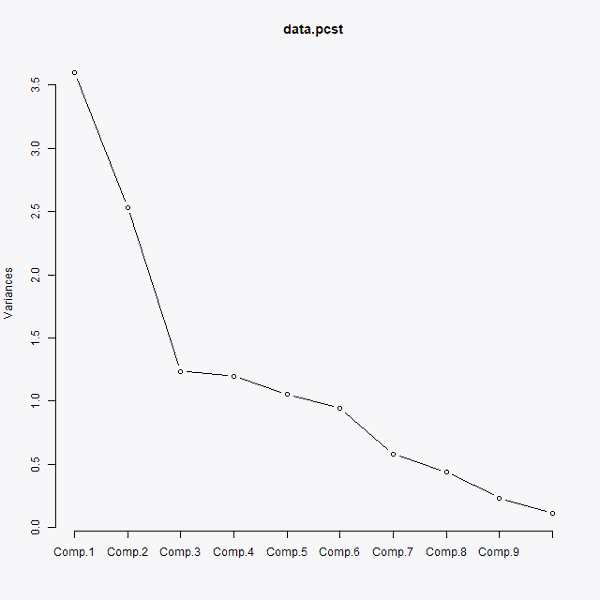
El primer paso de todos es observar mediante la siguiente gráfica cuántas componentes principales debemos coger.

Elección número de componentes principales

Como se ve en el gráfico anterior, las tres primeras componentes aglutinan la mayor varianza, por lo que podemos decir que son las componentes principales las principales para realizar el análisis. Sin embargo, para poder representar de forma bidimensional los resultados a lo largo de este post, escogeremos sólo las dos primeras. En el siguiente gráfico Podemos ver qué influencia ejerce cada variable en las nuevas componentes principales:

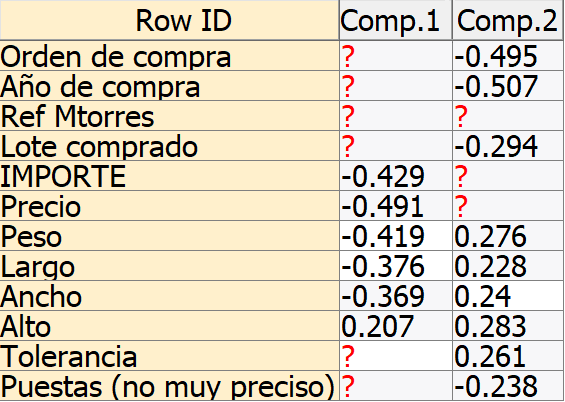
Influencia de cada variable en las dos componentes principales

Como podemos observar, las variables que más peso ejercen sobre la primera de las componentes principales son las medidas de las piezas, mientras que las variables que más peso ejercen sobre la segunda de las componentes principales son el resto de las variables, teniendo una mayor influencia el año en el que se realizó la compra y el número de la orden de la compra. Se podría decir que la primera componente principal representa las características de las piezas compradas mientras que la segunda componente principal representa las propiedades de la compra.

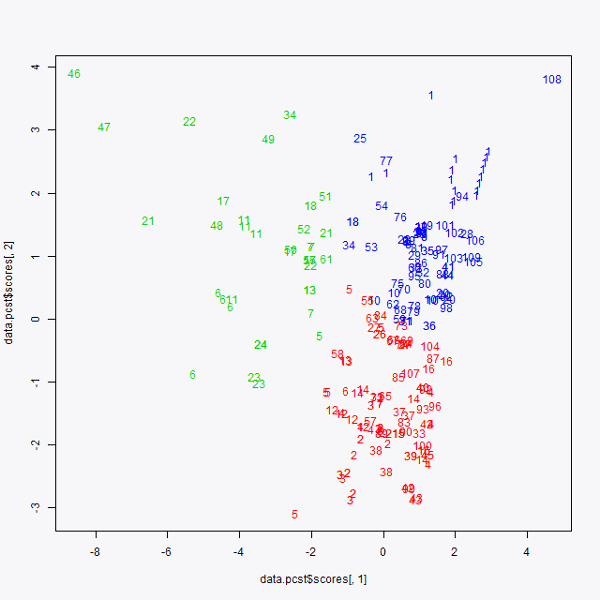
Una vez que se sabe que representa cada una de las variables, se representan en dos dimensiones. Se representa en el eje ‘x’ la primera de las componentes principales y en el eje ‘y’ la segunda de las componentes principales. De este modo se obtiene el gráfico 3. En él se puede observar la representación de los datos de inicio en dos dimensiones.

De esta forma, se puede hacer una interpretación de cada una de las órdenes de compra. Se puede ver que la orden de compra número 46 (arriba a la izquierda en el gráfico 3), al igual que la compra 108 (arriba a la derecha) podrían considerarse outliers. Pero sin duda, lo que más llama la atención de este gráfico es que más del 80% de los datos están condensados en dos grupos, destacados por dos círculos rojos. Esto nos indica que las órdenes de compra que no están próximas a estos grupos son las que provocan una varianza mayor en el precio de las órdenes de compra. Cuanto más a la derecha se encuentre una orden de compra más cara debe de ser y cuanto más a la izquierda se localice esta orden más barata ha de ser. Esto lo deducimos del gráfico 2 y cómo influye cada variable en las componentes principales.

Representación gráfica en las dos principales componentes

Clasificación de los datos por medio del algoritmo K-Means

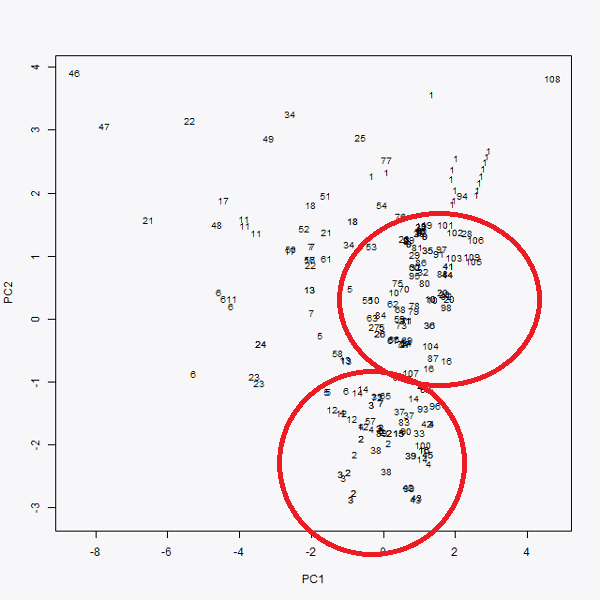
Una vez realizado esta representación gráfica, pasamos a utilizar el algoritmo K-means. Este algoritmo sirve para localizar grupos dentro de una “nube de puntos”, que en este caso son las compras. Se ha decidido agrupar los datos en tres grupos, por lo tanto, se está realizando el algoritmo K-means con K=3. El resultado obtenido es el siguiente:

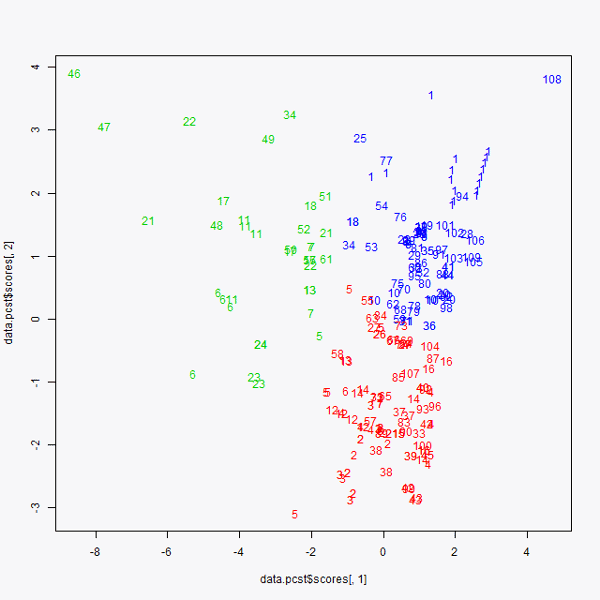
Gráfico K-means

Se obtienen, por consiguiente, tres grupos. Como se había mencionado primero, había dos grupos claramente diferenciados (ahora en rojo uno y en azul el otro) y, localizamos otro tercer grupo, formado por el resto de los puntos que representan todos los datos que se “salen” de los dos grupos de órdenes de compras mencionados previamente.

Para continuar con el análisis y sacar conclusiones más profundas e importantes, habría que realizar un análisis en profundidad sobre los datos del tercero de los grupos representados en color verde.

Conclusión

Cuando nos encontremos con multitud de variables que analizar, lo mejor es reducir estas variables al mínimo para poder representarlas de manera gráfica e intuitiva. Una vez hecho este paso, se pueden aplicar otro tipo de técnicas, como en este caso, que sirven para entender aún de forma más clara y explícita para qué usar los datos o cómo interpretarlos.

Este tipo de análisis de datos es muy útil para poder relacionar variables entre ellas y entender cómo están relacionadas. Aplicado a logística, por ejemplo, este estudio se puede aplicar también para decidir en qué lugar geográfico es mejor asentar un almacén. Si consideramos que los puntos de la última imagen son clientes finales y tenemos pensado construir tres almacenes desde donde distribuir los productos de una empresa, podremos saber el lugar óptimo dónde asentar los almacenes sería en el centro de cada uno de estos grupos, consiguiendo que la distancia desde el almacén a los clientes sean las mínimas.

COMPARTE ESTE POST

Share on facebook
Share on google
Share on twitter
Share on linkedin
Share on pinterest
Share on print
Share on email